2024. 6. 5. 14:20ㆍ수학 필기노트/선형대수
Determinants
N x N 행렬을 A라고 했을때, 행렬식 det(A)는 첫번째 행의 원소들 그에 따른 소행렬식의 곱의 합으로 정의된다.


위 A 행렬을 계산해보자.
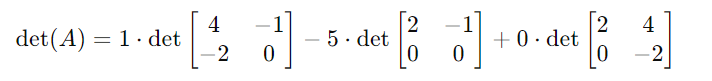
먼저 첫번째 행과 소행렬의 곱으로 나타낸 모습이다. 이중 3번째 소행렬과의 곱은 0이기 때문에 다음 계산에서 생략된다.
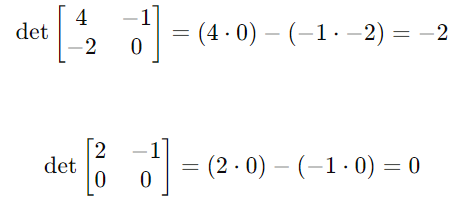
소행렬들의 determinant 값을 구한 모습. 첫번째는 -2, 두번째는 0이라는 결과가 나왔다.

위에 계산한 소행렬의 det값을 대입하여 나머지를 계산한다.
Properties of Determinants
행 연산에 따른 행렬식 변화
1. 한 행에 다른 배수를 더해도 행렬식은 변화하지 않는다.
2. 두 행을 바꾸면 행렬식의 부호가 변한다.
3. 한 행을 스칼라 k로 곱하면 행렬식은 k배가 된다
행렬 A가 가역 행렬일 필요충분 조건은 det(A) != 0
행렬 A의 전치 행렬 A^t의 행렬식은 A와 같다
Cramer's rule

해당 시스템을 크래머의 법칙으로 풀어보자.
크래머의 법칙에 따르면 시스템 Ax=b의 해는 밑의 식으로 구할 수 있다.

여기서 행렬 Ai 는 행렬 A의 i번째 열을 벡터 b로 대체한 행렬이다.
먼저 분모인 det(A)를 구해보자.

위에서 다뤘던 determinant를 통해 계산해보면 2가 나온다.
det(Ai)를 구하기 위해, 첫번째 열의 3, -5를 벡터 b인 6, 8로 바꾼다.

바꾼다음 determinant를 계산하면 40이 나온다.
2 / 40 = 20, 따라서 x1은 20이다.
x2를 구하기 위해 마찬가지로 2번째 열을 벡터 b로 바꾼다.

바꾼뒤 계산된 det(A2)의 값은 54가 나온다.
2 / 54 = 27, 따라서 x2는 54이다.

결과적으로, 크래머의 법칙으로 구한 x의 해는 위와 같다.
'수학 필기노트 > 선형대수' 카테고리의 다른 글
| 선형대수 - Inner Product, Length, and Orthogonality (내적, 길이, 그리고 직교성) (0) | 2024.06.10 |
|---|---|
| 선형대수 - Diagonalization (대각화) (0) | 2024.06.09 |
| 선형대수 - Eigenvalues and Eigenvectors (고유값과 고유벡터) (0) | 2024.06.09 |