선형대수 - Eigenvalues and Eigenvectors (고유값과 고유벡터)
2024. 6. 9. 13:09ㆍ수학 필기노트/선형대수
반응형
고유값과 고유벡터의 정의
정사각 행렬 A에 대해, 만약 v != 0인 벡터 v와 스칼라 λ가 존재하여 Av = λv를 만족한다면,
v를 A의 고유 벡터라고 하고 λ를 고유값이라고 한다.
고유값과 고유벡터를 찾는 방법
고유값과 고유벡터를 찾기 위해서는 다음 단계를 따른다 :
1. 특성 방정식 찾기

특성 방정식은 A 행렬에서 람다 스칼라를 뺀 뒤 determinant한 모양이다.
람다 스칼라와 행렬은 뺄 수 없으므로 람다 스칼라에 단위 행렬을 곱해준다.
2. 고유값 λ 찾기
위에서의 특성 방정식을 해결하여 고유값을 찾는다.
3. 고유벡터 v찾기
각 고유값에 대해 (A- λI)v = 0을 풀어 고유벡터를 찾는다.
고유값과 고유벡터 찾기 예제

위 행렬 A의 고유값과 고유벡터를 찾아보자.
먼저 특성 방정식을 찾는다.

det(A- λI) = 0에 A를 대입한 후 식을 전개한다.

와 같은 형태로 표현할 수 있다.

행렬끼리 계산하면 대각선에 있는 요소들에 - λ가 된다.
determinant를 계산하면

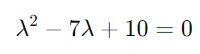
가 되어 위와 같은 2차 방정식이 나온다.
여기서 고유값은 저 λ의 해를 구하면 된다.
2차 방정식을 인수분해하면 ( λ - 2 ) ( λ - 5 )가 나온다.
따라서 고유값은 2와 5이다.
이제 고유벡터를 찾아보자. 먼저 고유값이 2일때의 고유벡터는
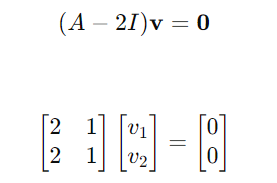
로 표현할 수 있다. 2를 곱한 단위 행렬을 A에서 빼면 위와 같은 형태가 되고
저 행렬이 0이 되려면 2x1 - 1x2 이기 때문에,

고유값이 5일때도 마찬가지로 구하면 된다.

반응형
'수학 필기노트 > 선형대수' 카테고리의 다른 글
| 선형대수 - Inner Product, Length, and Orthogonality (내적, 길이, 그리고 직교성) (0) | 2024.06.10 |
|---|---|
| 선형대수 - Diagonalization (대각화) (0) | 2024.06.09 |
| 선형대수 - Determinants (행렬식) (0) | 2024.06.05 |