2024. 6. 10. 13:52ㆍ수학 필기노트/선형대수
Inner Product
벡터 u = [u1, u2, u3 ...] 과 벡터 v = [v1, v2, v3 ...]의 내적 (inner product)는 아래와 같이 표현할 수 있다.

내적의 성질에는 교환법칙, 분배법칙이 적용된다.

벡터의 길이
벡터 v의 길이는 ||v|| 기호로 표현한다.
피타고라스 개념을 적용하여 아래 수식으로 벡터의 길이를 구한다.

Orthogonality (직교성)
두 벡터 u, v가 직교한다는 것은 u와 v를 내적한 값이 0이라는 소리다.
직교하는 두 벡터는 서로 수직이고, 서로 선형 독립이다.
orthogonal set
서로 직교하는 벡터의 집합을 의미하며, 집합 {v1, v2, v3.. } 등의 벡터가 서로 직교해야한다.
orthogonal basis
벡터 공간 V의 부분공간 W의 직교 기저(orthogonal basis)는 직교 집합인 기저 벡터들의 집합이다.

크기와 상관 없이, 벡터들이 서로 직교하기만 하면 된다.
orthonormal basis
orthogonal basis와 같이 벡터들이 서로 수직이고, 내적이 0이며, 벡터의 길이가 1인 경우
정규 직교 기저(orthonormal basis)라고 한다.
orthogonal projection
벡터 v를 벡터 u에 직교 투영(orthogonal projection) 한 결과는 다음과 같이 정의된다.

투영 벡터는 원래 벡터와 투영 벡터 사이의 각도를 유지하고,
투영 벡터와 원래 벡터 사이의 차이는 직교한다.
예시로 벡터 v = [3 4]를 벡터 u = [1 2]에 orthogonal projection을 해보자.
먼저 v 와 u 의 내적을 계산한다.
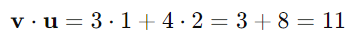
그 뒤로 u의 내적을 계산한다.


식에 대입하면 다음과 같은 투영 벡터가 나온다.
Gram-Schmidt Process
그람-슈미트 과정은 주어진 벡터 집합을 모두 직교로 변환하는 방법이다.
주어진 벡터 {v1, v2, v3}을 직교 벡터 집합 {u1, u2, u3}로 다시 만들어보자.
먼저 기준이 되는 첫번재 벡터를 선택한다.
그러므로 u1과 v1은 같다.

두번째 벡터 u2는 v2에서 u1에 대한 투영 벡터를 뺀 결과이다.


세번째 벡터 u3는 v3에서 u1과 u2에 대한 투영 벡터를 빼면 된다.


정리하면, n번째 벡터 Un은 Vn 에서 이전 n-1 개의 직교 벡터들에 대한 투영 벡터들을 뺀 결과이다.

왜 투영 벡터를 빼는가?
투영 벡터를 빼는 이유는 새로운 벡터가 이전에 직교화된 벡터들과 직교하기 위함이다.
벡터 Vn에서 이전 벡터들에 투영한 벡터들을 빼면 남은 Un은 이전 벡터들과 직교하게 되기 때문이다.
'수학 필기노트 > 선형대수' 카테고리의 다른 글
| 선형대수 - Diagonalization (대각화) (0) | 2024.06.09 |
|---|---|
| 선형대수 - Eigenvalues and Eigenvectors (고유값과 고유벡터) (0) | 2024.06.09 |
| 선형대수 - Determinants (행렬식) (0) | 2024.06.05 |