[수2] 01. 함수의 극한
2019. 8. 8. 14:22ㆍ수학 필기노트/수학Ⅱ
반응형
함수의 극한과 수렴
함수 f(x)에서 x의 값이 a와 다른값을 가지면서 a에 한없이 가까워질 때, f(x)의 값이 일정한 값 알파에 한없이 가까워지면,
함수 f(x)는 알파에 수렴한다고 하고 이것을 수식으로 나타내면 밑의 수식과 같다.
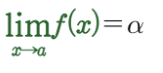
이때 알파를 x=a 에서의 극한값 또는 극한이라고 부른다.
극한의 존재성
함수의 극한에서, x의 값이 a보다 크면서 a에 한없이 가까워 지는것을 우극한, 기호로 x -> a+ 로 나타내고
x의 값이 a보다 작으면서 a에 한없이 가까워 지는것을 좌극한, 기호로 x-> a- 로 나타냅니다.
따라서 우극한 또는 좌극한이 하나라도 존재하지 않거나, 그 값이 다르다면 극한값은 존재하지 않습니다.
극한의 성질
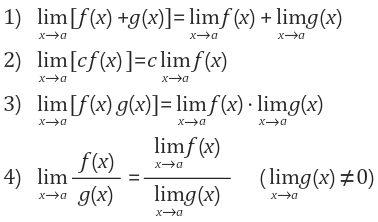
다음은 극한의 성질으로, 어떤 함수의 합, 차, 실수배, 곱 형태인 극한을 그래프를 사용하지 않고,
극한값을 이용하여 계산할 수 있는 공식이다.
이 공식들은 f(x), g(x)가 각각 수렴해야 위의 성질이 성립하게 된다.
그리고 좌극한과 우극한, x -> 무한, x -> -무한 일때도 모두 성립한다.
극한의 대소 관계
다음에서 limf(x)와 limg(x)가 실수일때,
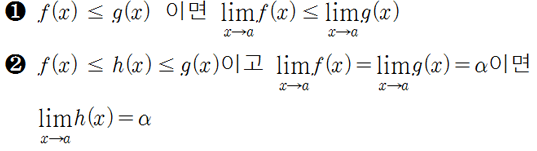
라는 공식이 성립한다.
위의 대소관계는 좌극한과 우극한, x -> 무한, x -> -무한 일때도 모두 성립하고,
2번의 공식은 양옆 극한값이 같으면 가운데도 같아진다하여 샌드위치 정리라고 부르기도 한다.
반응형
'수학 필기노트 > 수학Ⅱ' 카테고리의 다른 글
| [수2] 05. 함수의 극대와 극소, 그래프 (0) | 2019.08.12 |
|---|---|
| [수2] 04. 접선의 방정식, 평균값 정리 (0) | 2019.08.12 |
| [수2] 03. 미분계수와 도함수 (0) | 2019.08.08 |
| [수2] 02. 함수의 연속 (0) | 2019.08.08 |
| 수학 학습정리를 시작합니다. (0) | 2019.05.11 |