[수2] 06. 도함수의 활용
2019. 8. 12. 09:45ㆍ수학 필기노트/수학Ⅱ
반응형
함수의 최대와 최소
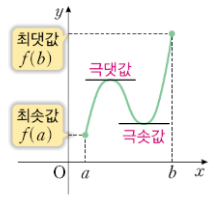
닫힌구간 [a,b]에서 연속인 함수f(x)의 최댓값/최솟값은 다음과 같은 순서로 구할 수 있다.
1. 주어진 구간에서 f(x)의 극댓값과 극솟값을 모두 구한다.
2. 주어진 구간의 양 끝 f(a) , f(b)를 구한다.
3. 극댓값, 극소, 위에서 구한f(a)와 f(b)를 통틀어 가장 큰게 최댓값, 가장 작은게 최솟값이다.
방정식에서의 도함수 활용
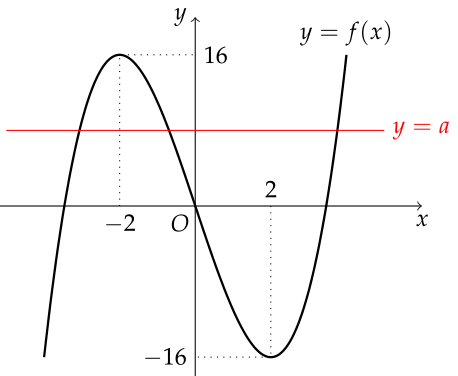
방정식 f(x) = 0의 서로 다른 실근의 개수는 함수 f(x)의 교점의 개수와 같은점을 이용하여,
방정식을 미분하여 값을 구할 수 있다.
부등식에서의 도함수 활용

방정식과 마찬가지로 부등식을 미분하여 범위를 증명해낸다.
속도와 가속도

위치가 x=f(t)일때,
속도v는 f(t)를 미분한 식이고,
가속도는 v(t)를 미분한 식으로 나타낼 수 있다.
시각에 대한 변화율
또한 길이, 넓이, 부피의 변화율도 알아낼 수 있다.

시각에 따른 변화율은,

로 나타낼 수 있다.
반응형
'수학 필기노트 > 수학Ⅱ' 카테고리의 다른 글
| [수2] 08. 정적분 (0) | 2019.08.13 |
|---|---|
| [수2] 07. 부정적분 (0) | 2019.08.12 |
| [수2] 05. 함수의 극대와 극소, 그래프 (0) | 2019.08.12 |
| [수2] 04. 접선의 방정식, 평균값 정리 (0) | 2019.08.12 |
| [수2] 03. 미분계수와 도함수 (0) | 2019.08.08 |