2024. 10. 19. 17:38ㆍ수학 필기노트/이산수학
무한 집합의 기수성 (Infinite Cardinalities)
기수성은 집합의 원소 개수를 나타내는 수치로, 특히 무한 집합의 경우 전단사 함수를 통해 정의됩니다.
두 집합 A와 B가 동일한 기수성을 가진다는 것은, 두 집합 사이에 전단사 함수(bijection)가 존재함을 의미합니다.
이는 두 집합의 원소들이 1:1로 대응될 수 있다는 뜻입니다.
유한 집합의 경우, 두 집합이 동일한 원소의 개수를 가질 때 기수성이 같다고 말합니다.
무한 집합에서도 이와 동일한 원칙이 적용됩니다.
가산 무한 집합과 비가산 무한 집합 (Countable / Uncountable Sets)
가산 집합 : 집합이 유한하거나 자연수 집합과 1:1 대응이 가능한 무한 집합을 말한다.
자연수 집합 N, 정수 집합 Z 등이 가산 집합이다.
비가산 집합 : 집합이 자연수 집합과 1:1 대응이 불가능할 때, 원소들을 나열할 수 없을 때 비가산 집합이다.
실수 집합 R은 비가산 집합이다.
가산 집합의 예시 (Example of Countable Sets)
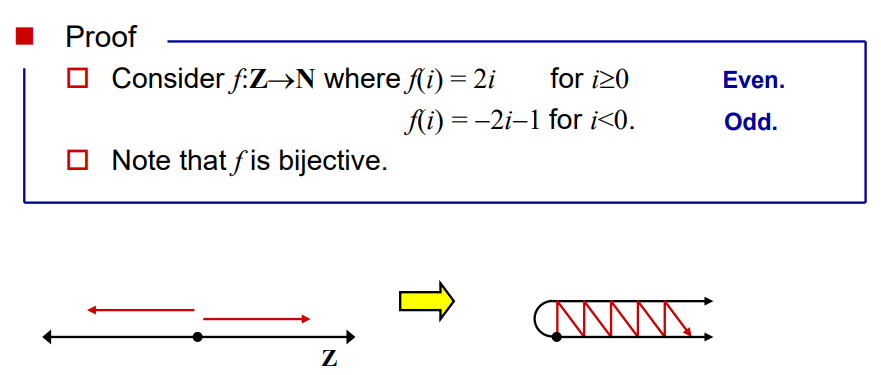
정수 집합이 가산 무한 집합임을 보이기 위해 함수 f: Z→N 을 정의합니다.
이 함수는 정수 가 0 이상일 때 f(i) = 2i , 음수일 때 로 나타낼 수 있습니다. 이 함수는 전단사 함수로, 정수 집합과 자연수 집합이 1:1 대응할 수 있음을 보여줍니다.
비가산 집합의 예시 (Example of Uncountable Sets)
실수 구간 [0, 1)을 칸토어의 대각선 논법을 통해 비가산 집합임을 증명할 수 있다.
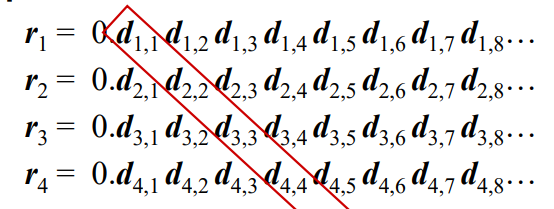
[0, 1) 구간 내의 실수를 나열하려고 할 때, 그 실수들의 각 자리 숫자를 사용해
대각선 방향으로 새로운 실수를 만듭니다. 이 실수는 나열된 실수 중 어느 것도 포함되지 않으므로,
원소를 완전하게 나열할 수 없다는 사실을 증명할 수 있습니다.
'수학 필기노트 > 이산수학' 카테고리의 다른 글
| [이산수학] 수열과 합 (0) | 2024.10.19 |
|---|---|
| [이산수학] 함수 (0) | 2024.10.19 |
| [이산수학] 집합 연산자 (0) | 2024.10.19 |
| [이산수학] 집합 (0) | 2024.10.19 |
| [이산수학] 중첩 한정자 (0) | 2024.10.15 |