[미적분] 03. 수열의 극한값 계산
2020. 1. 31. 21:31ㆍ수학 필기노트/미적분
반응형
수악중독님의 교재를 참고하여 작성하였습니다. 학생이다 보니 틀린점이 있으면 마음껏 지적해주세요
수식은 mathjax api를 사용하였습니다
오늘 알아볼것은, 수열이 발산할때 극한값을 계산하는 방법이다.
먼저 $\infty \over \infty$ 같은 분수꼴이 나온다면, 분모의 최고차항으로 분모와 분자를 나누어 계산한다.

그럼 다음과 같은 결과가 나오게 되는데 이 원리들은 예제를 풀며 이해를 해보자.
#1 분자의 차수 > 분모의 차수 예제

분모의 최고차항으로 나누면 최고차항이 일차이기 때문에 n으로 나누면 된다.
그러면
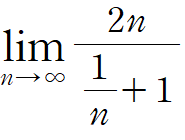
와같이 나누어진다.
여기서 무한으로 늘어난다면, 분모는 1에 가까워지고 분자는 무한에 가까이 늘어나므로,
극한값은 $\infty$이라는것을 알 수 있다.
#2 분자의 차수 = 분모의 차수 예제

분모의 최고차항이 이차이기 때문에 나누면,
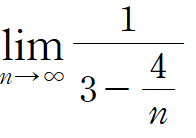
가 된다.
$4 \over n$에서 n이 무한으로 커지면 0에 수렴하기 때문에, $1 \over 3-0$이 된다
극한값은 $1 \over 3$
#3 분자의 차수 < 분모의 차수 예제
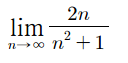
분모의 최고 차항으로 나누면,

가 된다.
$x \over n$꼴은 무한으로 갈수록 0에 수렴하기 때문에 분자가 0이 되서
극한값은 0이다.
반응형
'수학 필기노트 > 미적분' 카테고리의 다른 글
| [미적분] 06. 급수의 수렴과 발산 (0) | 2020.02.17 |
|---|---|
| [미적분] 05. 등비수열의 극한 (0) | 2020.02.11 |
| [미적분] 04. 수열의 극한의 대소관계 (0) | 2020.02.07 |
| [미적분] 02. 수열의 극한 성질 (0) | 2020.01.29 |
| [미적분] 01. 수열의 수렴과 발산 (0) | 2020.01.22 |